Математика, а геометрия в частности, согласно опросам школьников, один из самых нелюбимых уроков, а все потому, что заставляют учить огромное количество формул, которые в жизни 90% из нынешних взрослых так и не нашли практического применения. Но, на минуточку, мы учим формулы, решаем задачи, делаем уравнения не для того, что они могут нам пригодиться в жизни, а потому как это развивает мышление и логику. Еще древнегреческие мудрецы говорили, что интеллект человека можно измерить по знаниям математических наук. И раз уж вы решили ознакомиться с применением формул по равнобедренному треугольнику – берем себя в руки и читаем статью целиком.
Прежде чем приступатьк ответу на вопрос как найти площадь равнобедренного треугольника и перейти к практической части статьи, где приведены формулы и расчеты, давайте обозначим для себя само понятие. Равнобедренный треугольник – это треугольник, в котором равны по длине две из трех сторон, которые называются боковыми. В случае с правильным треугольником, где все стороны равны, он тоже считается равнобедренным, однако наоборот, когда равнобедренный треугольник считают правильным – неверно.
Стороны треугольника следует обозначить, сделаем это таким образом, как представлено на картинке ниже, где: а – боковые стороны, b-основание, а h-высота.
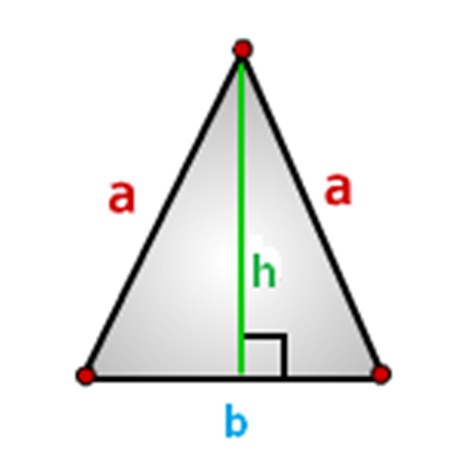

Как рассчитать площадь равнобедренного треугольника, формулы.
После того, как мы сделали обозначения высоты, сторон и угла, можно приступить к решению задачи.
Для начала, определим, что нам известно.
Если высота и основание – то подойдет классическая формула (*- знак умножения):
S = ½ *b*h
Подставим, для примера, числа, где: h=16, b=18, получаем следующее:
S = ½ *18*16=9*16=144;
Площадь равнобедренного треугольника S=144 см2
Существуют и другие формулы, которые помогут нам в том, как узнать площадь равнобедренного треугольника. Одной из таких формул является метод Герона. Не будем писать сложную формулу, возьмем, за основу, сокращенную:
S = ¼ b √4*a2-b2
Понятно, что b – основание, а — равные стороны. Формула подходит в том случае, когда h-высота неизвестна.
Подставляем значения, пусть a=6, b=3, получаем следующее:
S= ¼ *3 √4*62-32= ¾ √144-9 = ¾ * 9 = 8,7
Можно использовать, чтобы высчитать площадь, равные стороны треугольника и угол между сторонами:
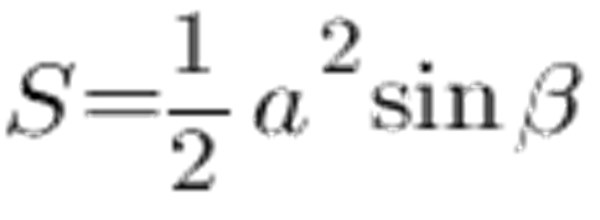
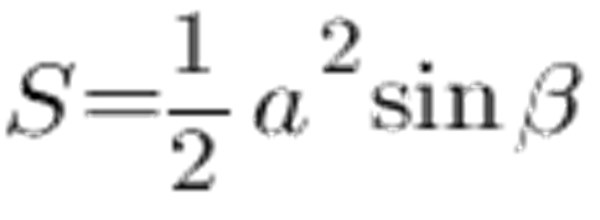
По таблице синусов угол в 45о равняется 0,7071, сторона а пусть будет равна 6 см, получаем следующее:
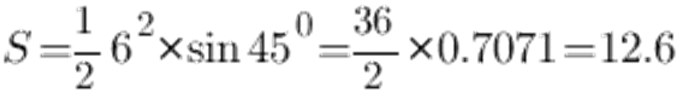
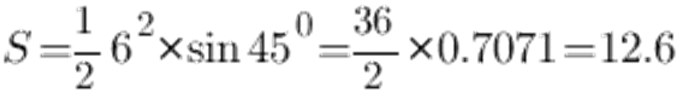
Как итог, площадь равнобедренного треугольника равна 12,6 см2.
Существуют еще способы расчета площади, в том числе и применительно к равнобедренному треугольнику, однако они достаточно сложны и не применяются в «элементарных», по понятием сложной математики, расчетах, типа приведенных выше. А говорить о вещах, которые не поймут даже преподаватели со стажем – не стоит.
Так что, можно вздохнуть с облегчением, на этом небольшой курс геометрии по нахождению площади равнобедренного треугольника будем считать оконченным, а знания, полученные в результате прочтения статьи – усвоенными на «пять».